Определенный интеграл, в отличие от неопределенного, имеет в итоге числовое значение.
Определенный интеграл |
Определенный интеграл как предел интегральной суммы |
| b | | n - 1 | |  | f(x)dx= | lim | ( | ∑ | f( | |
i | )Δx |
i | ) , | | a | | | | i = 0 | |
|
| где | |
i | ∈ | [x |
i | , x |
i + 1 | ] и Δx |
i | = x |
i + 1 | - x |
i |
|
Формула Ньютона - Лейбница: если f(x) непрерывна и F'(x) = f(x), то |
| b | |  | f(x)dx = F(b) - F(a) | | a | |
|
Основные свойства определенного интеграла |
| b | | b | |  | f(x)dx = |  | f(t)dt | | a | | a | |
|
| a | |  | f(x)dx = 0 | | a | |
|
| b | | a | |  | f(x)dx = − |  | f(x)dx | | a | | b | |
|
| c | | b | | b | |  | f(x)dx + |  | f(x)dx = |  | f(x)dx | | a | | c | | a | |
|
| b | | b | |  | k f(x)dx = k |  | f(x)dx | | a | | a | |
|
| b | | b | | b | | b | |  | (f(x) + g(x) - h(x))dx = |  | f(x)dx + |  | g(x)dx − |  | h(x)dx | | a | | a | | a | | a | |
|
| x | | d
dx |  | f(t)dt = f(x) | | a | |
|
| b | | d
dx |  | f(t)dt = −f(x) | | x | |
|
Теорема о среднем. Если f(x) непрерывна на [a, b], то |
| b | |  | f(x)dx = (b - a)f(c) , | | a | |
|
| где a < c < b |
Формула интегрирования по частям в определенном интеграле |
| b |  | | a |
| u(x)V'(x)dx = u(x)V(x) | 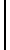 | b
a | - | | b |  | | a |
| V(x)u'(x)dx |
|
Формула замены переменной в определенном интеграле |
| φ(β) |  | | φ(α) |
| f(x)dx = | | β |  | | α |
| f(φ(t))φ'(t)dt |
|
Формула трапеции |
| b |  | | a |
| ydx = h( | 1
2 | y |
0 | + y |
1 | + ... + y |
n - 1 | + | 1
2 | y |
n | ) , |
|
| где h = | b - a
n | , x |
0 | = a и x |
n | = b, y = f(x), y |
i | = f(x |
0 | + ih) (i = 0, 1, 2, ..., n) |
|
Формула Симпсона |
| b |  | | a |
| ydx = | h
3 | (y(a) + 4y( | a + b
2 | ) + y(b)) , где h = | 1
2 | (b - a) |
|
Несобственный интеграл |
| +∞ |  | | a |
| f(x)dx = |
lim
b → +∞ | | b |  | | a |
| f(x)dx |
|
Площадь криволинейной трапеции, ограниченной непрерывной линией
y = f(x) (f(x) ≥ 0), осью Ox и двумя вертикалями x = a и x = b (a < b) |
| S = | | b |  | | a |
| ydx |
|
Площадь сектора, ограниченного непрерывной линией ρ = f(φ)
(ρ и φ - полярные координаты) и двумя лучами φ = α и φ = β (α < β) |
| S = | 1
2 | | β |  | | α |
| ρ | 2
| dφ |
|
Длина дуги гладкой кривой y = f(x) в прямоугольных координатах
x и y от точки x = a до точки x = b (a < b) |
| l = | | b |  | | a |
| √ | | dx |
|
Длина дуги гладкой кривой ρ = f(φ) в полярных координатах
ρ и φ от точки φ = α до точки φ = β (α < β) |
| l = | | β |  | | α |
| √ | | dφ |
|
| Длина дуги гладкой кривой x = φ(t), y = ψ(t), заданной параметрически (t |
0 | < T) |
|
| t = | | T |  | |
| √ | | dt |
|
Объем тела с известным поперечным сечением S(x) |
| V = | | b |  | | a |
| S(x)dx |
|
Объем тела вращения |
| - вокруг оси Ox: V |
x | = π | | b |  | | a |
| y | 2
| dx (a < b) |
|
| - вокруг оси Oy: V |
y | = π | | d |  | | c |
| x | 2
| dy (c < d) |
|
Работа переменной силы F = F(x) на участке [a, b] |
| A = | | b |  | | a |
| F(x)dx |
|